[백준] 2178번 파이썬 (Python) 풀이

문제

N×M크기의 배열로 표현되는 미로가 있다.

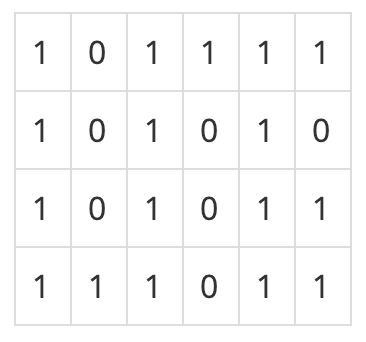
미로에서 1은 이동할 수 있는 칸을 나타내고, 0은 이동할 수 없는 칸을 나타낸다. 이러한 미로가 주어졌을 때, (1, 1)에서 출발하여 (N, M)의 위치로 이동할 때 지나야 하는 최소의 칸 수를 구하는 프로그램을 작성하시오. 한 칸에서 다른 칸으로 이동할 때, 서로 인접한 칸으로만 이동할 수 있다.

위의 예에서는 15칸을 지나야 (N, M)의 위치로 이동할 수 있다. 칸을 셀 때에는 시작 위치와 도착 위치도 포함한다.

(출처: 2178)

입력

첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.

출력

첫째 줄에 지나야 하는 최소의 칸 수를 출력한다. 항상 도착위치로 이동할 수 있는 경우만 입력으로 주어진다.

예제 입력 1

4 6
101111
101010
101011
111011

예제 출력 1

15

---

풀이

 

 

- BFS 기본 문제다. BFS와 DFS 개념을 알아야 한다.

- dx, dy를 두고 현재 위치를 기준으로 상, 하, 좌, 우를 탐색하도록 했다.

- nx, ny가 다음에 갈 좌표를 나타낸다. 다음 갈 좌표의 값이 1일 경우 (현재 위치 + 1)한 값으로 바꾸어준다.
이렇게 계속 진행하면 최종 (n, m)에는 지나온 칸 수의 합이 나오게 된다.

from collections import deque

n, m = map(int, input().split())

graph = []
for i in range(n):
    graph.append(list(map(int, input())))

# 현재 좌표 기준 상, 하, 좌, 우 탐색
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]


def bfs(x, y):
    q = deque()
    q.append((x, y))

    while q:
    	# (x, y) 방문 -> 큐에서 삭제
        x, y = q.popleft()
        # 상,하,좌,우 탐색하니 4번 반복
        for i in range(4):
        	# next x,y에 현재 위치 + 상,하,좌,우
            nx = x + dx[i]
            ny = y + dy[i]
			
            # 값이 허용범위를 넘거나 좌표의 값이 0일 경우 아무 동작하지 않음
            if nx < 0 or nx >= n or ny < 0 or ny >= m:
                continue
            if graph[nx][ny] == 0:
                continue
            if graph[nx][ny] == 1:
            	# 현재 좌표 기준 다음 단계의 값을 (현재 좌표의 값 + 1)으로 바꿈
                graph[nx][ny] = graph[x][y] + 1
                # 지금 큐에 넣는 nx, ny는 다음 반복 시 현재 값으로 사용됨. 
                q.append((nx, ny))
    # 마지막 좌표의 값을 리턴
    return graph[n - 1][m - 1]


print(bfs(0, 0))